Voltage
divider :
il partitore di tensione
|
Calcolare il partitore
Per chi è pigro, o semplicemente non vuole impegnare tempo, basta
inserire "voltage
divider calculator" in Google per ottenere numerose pagine che
offrono un foglio di calcolo o un' applet automatizzata per il calcolo di
R1 e R2. Il che è molto comodo nella pratica.
Vediamo comunque alcuni esempi di calcolo.
Calcolo per i partitori resistivi
Ad esempio, se abbiamo in ingresso una Vin = 10V e vogliamo in uscita
una Vout = 5V, il rapporto di divisione sarà:
Vout / Vin = 5 / 10 = 1/2
ovvero:
R2 / (R1 + R2) = 1/2
da cui:
R1 = R2
Se il rapporto assume valori differenti, sarà possibile
risolvere la (5) sia per R1 che per R2
R1 = ((R2 * Vin) / Vout ) - R2
R2 = R1 / (( Vin / Vout) -1)
Ad esempio, se abbiamo una tensione di 12V massimi e dobbiamo
riportarla ai 5 V dell' ingresso del modulo ADC del microcontroller, il fattore di
divisione
sarà:
Vout / Vin = 5 / 12 = 0,4167
Potremo utilizzare, prendendo i valori dalla serie E24 una
R1
= 1800 Ω con una R2 = 1300 Ω (oppure 18k e 13k), con un errore dell' ordine dello 0.6%, mentre
utilizzando valori della serie E96 potremo impiegare le coppie :
R1
[Ω] |
R2
[Ω]
|
| 1400 |
1000 |
| 2800 |
2000 |
| 3570 |
2550 |
| 10500 |
7500 |
| 51100 |
36500 |
| 105000 |
75000 |
e altre ancora, con i relativi multipli o sottomultipli, con un errore di divisione dello 0%.
Questo è possibile dato che:
|
la tensione di uscita, fissata
una tensione di ingresso, dipende dal rapporto tra R1 e R2.
E', quindi,
evidente che si potranno scegliere diversi valori per R1 e R2 che forniscono
il rapporto desiderato.
|
Ad esempio, se occorre dividere la tensione a metà, ovvero R1 = R2
, si
potranno utilizzare due resistori da 10k o da100k o da 1k o qualsiasi altra coppia di
resistenze dello stesso valore.
Allora, quale valore scegliere ?
Dobbiamo considerare due punti:
-
Più piccolo sarà il valore
delle resistenze, maggiore sarà la corrente I che le attraversa
e quindi il carico sulla sorgente di tensione e la dissipazione di
potenza.
Di conseguenza, il valore delle resistenze dovrà essere non
minore della resistenza di uscita della sorgente della Vin, così da non
sovraccaricarla.
In particolare, per applicazioni a basso consumo o in sistemi alimentati a
batteria, basse correnti sono sempre auspicabili.
-
Per contro, se utilizziamo valori molto elevati per le resistenze, ci possiamo trovare ad
alimentare la Vout con una impedenza elevata (dovuta al valore
di R1 che si trova in serie alla tensione di uscita); questa potrebbe essere eccessiva
rispetto a quella dell' ingresso a cui la Vout va applicata, con il risultato
di non poter fornire la corrente adeguata e, in sostanza, alterare il rapporto
di divisione, come vediamo più a vanti nel paragrafo dedicato al partitore
caricato.
Un approccio percentuale.
Possiamo considerare anche il partitore in funzione del
suo rapporto di divisione:
Vout / Vin
è pari al rapporto tra la tensione ai capi della
resistenza considerata e la tensione complessiva ai capi della serie.
Il che vuol dire, essendo la corrente che le attraversa la medesima, che
il rapporto di divisione è lo stesso rapporto che c' è tra la resistenza
e la somma delle resistenze:
Vout / Vin = R2 / (R1 + R2)
Quindi possiamo considerare le espressioni in forma
percentuale, essendo il 100% la somma delle resistenze, il che è come
dire la tensione di alimentazione della serie.
| La differenza di potenziale ai capi di ciascuna
resistenza del circuito in serie è direttamente proporzionale al rapporto tra
il valore della resistenza considerato e la resistenza totale equivalente del circuito in serie.
|
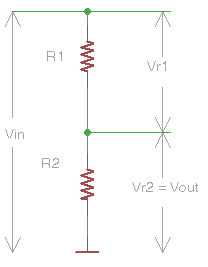 |
Quindi, ad esempio, se :
R1 = 20% (R1+R2)
e R2 = 80% (R1+R2)
avremo che:
Vr1 = 20% (Vr1+Vr2) = 20% Vin
Vr2 = 80% (Vr1+Vr2) = 80% Vin
e
quindi:
Vr2 / Vin = 20/80 = 1/4
|
Ad esempio, se si vuole ottenere Vout / Vin = 1/2,
ne deriva, senza calcoli particolari, che R2 = 50% del
valore complessivo della serie e quindi R1 = R2 e scegliere il valore
resistivo più adeguato all' applicazione.
Se si vuole ottenere Vout / Vin = 2/3, si
avrà:
Vr1 = 25 % Vin e Vr2 = 75% Vin
e altrettanto si potrà dire delle resistenze. In
relazione alla somma R1+R2,
R1 = 25% (R1 + R2) e R2
= 75% (R1 + R2)
Così, per un valore della serie (R1 + R2) di 10kΩ,
sarà
R1 = 25% (R1 + R2) = 25% 10k = 2500
Ω
e
R2 = 75% (R1 + R2) = 75% 10k
= 7500
Ω.
Questo genere di valutazione rende semplice il calcolo del
partitore in molte applicazioni.
Calcolo per i partitori in
ca.
Un breve cenno ai partitori per correnti alternate: in modo
del tutto analogo a quanto finora visto sarà possibile calcolare partitori i
cui elementi sono impedenze. Ad esempio, un partitore con
rapporto 1/3 potrà essere realizzato sia con R1 = 2 * R2, sia
con Z1= 2 * Z2. Per cui si potranno utilizzare due resistori: R1
= 10 kΩ e R2 = 5kΩ

|
oppure due induttanze, ad esempio:
L1 = 100 uH e L2 = 50
uH In questo caso, anche se la tensione di uscita non dipende dalla frequenza
della tensione in ingresso, se la reattanza degli induttori Xl
= ω L non è sufficientemente elevata, ci sarà una forte corrente
shuntata dalla L2.
Dovrebbe anche essere evidente che in continua un simile circuito si
comporta come un corto circuito, che, nella pratica, si trova con la
corrente limitata solo dalla resistenza dell' avvolgimento L1.
|

|
Nel caso di capacità, dobbiamo considerare che l'
impedenza capacitiva è funzione inversa della frequenza. La reattanza del
condensatore è: Xc = 1 / ω C per
cui l' impedenza è: Zc = j Xc
Quindi, nel caso in cui vogliamo risolvere la (6) in funzione delle
capacità, si deve notare che l' elemento in serie C1
va al numeratore:
Vout = Vin * C1 / (C1 + C2) |
Mentre se svolgiamo in base alle impedenze, la relazione (7)
è comunque valida.
Calcoli di partitori complessi utilizzanti contemporaneamente R-L-C
richiedono calcoli altrettanto complessi che non sono oggetto di queste
pagine.
|