|
Digitale e Analogico
Occorre allora avere ben chiare due definizioni:
- Analogico: viene chiamato analogica una grandezza i cui
valori sono continui. Così, se prendiamo in considerazione un certo intervallo di
tempo, il valore varia da A a B attraverso un numero
infinito di passi.
Ad esempio, un piano inclinato porta dal livello A al livello B in modo
continuo.
Analogica è l' incisione della musica in un disco di vinile.
- Digitale : viene riferito a quanto è rappresentabile con numeri
finiti. Il nome deriva deriva dall' inglese digit, che significa
cifra, che a sua volta deriva dal latino digitus, che significa dito
(inteso come mezzo più semplice di supporto al contare).
Digitale è contrapposto ad analogico, cioè il numerabile al non
numerabile.
Se vogliamo visualizzare un esempio pratico, "digitale" è una scala
che porta dal livello A al livello B
attraverso un dato numero di gradini, mentre "analogicamente"
avremmo lo stesso passaggio dal livello A a quello B attraverso un piano
inclinato.
Digitale è l'incisione della musica in un CDROM.
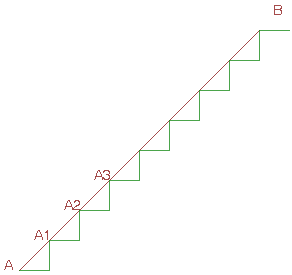 |
Nell' esempio della scala e del piano inclinato abbiamo l' essenza della
differenza tra digitale ed analogico.
Per andare da A a B:
-
Digitale si muove per passi (step, gradini), come su una scala
-
Analogico fluisce con continuità, come un piano inclinato.
Per passare dal livello A al livello A3, la scala ha tre gradini di altezza
ben definita, ai livelli A1, A2, A3; non ci sono possibilità intermedie. Per lo
stesso percorso, sul piano inclinato sono possibili tutti i punti del segmento
tra A e A3.
|
Ma quello che è importante considerare è che
entrambi i mezzi sono utilizzabili per passare dal
livello A a quello B,
quindi sono alternativi quando li
impieghiamo in un determinato ambito pratico. E questo ci consente di utilizzare i sistemi digitali per il controllo di
grandezze analogiche attraverso l' impiego di elaboratori (microprocesori,
microcontroller, ecc.), i quali operano su grandezze digitali.
Sappiamo che la risoluzione numerica di un elaboratore dipende dal numero dei
bit utilizzati: con 8 bit, ad esempio, potrò rappresentare (codificare) numeri interi da 0 a
255 (28 = 256), oppure numeri tra -128 e +127 se si utilizzano
codifiche per numeri con segno,
ma non gli infiniti valori frazionari tra uno e l' altro intero; per tornare
all' esempio precedente, con 8 bit la mia scala avrà 256 gradini.
Per poter rappresentare
numeri con definizione maggiore si rende necessario utilizzare un numero maggiore di
bit; ad esempio, con 16 bit il limite si sposta a 65535 e così via.
(Informazioni dettagliate
sui sistemi numerici qui.)
Per comprendere meglio il concetto, facciamo un esempio.
Una tensione varia tra 0 e 8V e sono disponibili sul sistema digitale 3 bit per
rappresentare il valore della tensione.
Questa, analogica, potrà assumere qualsiasi valore tra 0
e 8 V, ad esempio 1 o 3,456 o 7,62 V, ecc.
Ma il convertitore in uscita disporrà solamente di 3 bit per rappresentare il
numero corrispondente al risultato della conversione.
Poichè 23 = 8,
sono possibili solo 8 valori digitali in corrispondenza degli infiniti valori
analogici.
Quindi, a fronte di un "piano inclinato" analogico, abbiamo una
scala "digitale" di 8 gradini.
Se pensiamo egualmente spaziati i "gradini" digitali, distanti 1 V uno
dall' altro, abbiamo che:
Tensione
ingresso
[V] |
Uscita
digitale
3 bit |
| Vin < 1 |
000 |
| 1 ≤ Vin < 2 |
001 |
| 2 ≤ Vin < 3 |
010 |
| 3 ≤ Vin < 4 |
011 |
| 4 ≤ Vin < 5 |
100 |
| 5 ≤ Vin < 6 |
101 |
| 6 ≤ Vin < 7 |
110 |
| 7 ≤ Vin < 8 |
111 |
Un valore di ingresso di 0.1 o 0.5 o 0.98 V darà come uscita sempre 000 in
uscita.
Un valore di ingresso di 6.2 o 6.53 o 6.8 V darà sempre una uscita digitale di 110. E così
via.
Ovvero andrà persa una parte della dinamica dei valori di
ingresso. Se vogliamo un esempio meccanico, è come misurare una lunghezza con
un righello che abbia la minima divisione in cm: i millimetri non potranno
essere apprezzati. Per una definizione maggiore dovrò aumentare le divisioni
della scala, con i mezzi centimetri, i millimetri e così via.
E' molto importante fermarsi un attimo e considerare che tutto questo non ha nulla di strano o sorprendente
dato che, in
effetti, anche la definizione di un numero "analogico" dipende dalle
cifre che ho a disposizione per
rappresentarlo.
Così, certamente i numeri tra 1
e 2 sono infiniti, ma se ho solo due cifre disponibili per la rappresentazione,
potrò scrivere
1 1,1 1,2 1,3
1,4 1,5
ecc., ma non 1,12 o 1,253, che richiedono rispettivamente 3
e 4 cifre.
Dunque basterà aumentare il numero degli scalini (bit) in cui è resa la
conversione e si aumenterà la definizione. Con un numero molto elevato di gradini, tendente all'
infinito, eguaglierò la retta.
Ovviamente un numero infinito di gradini è irrealizzabile nella pratica e non avrebbe
neppure senso. Perchè ? Perchè se, teoricamente, gli elementi sono infiniti, occorre
avere ben presente che, all' atto
pratico, le nostre misure sono tutte "finite" e soggette ad un certo
errore.
E la dipendenza dal metodo di misura e dagli strumenti usati è fondamentale.
Con l' esempio del righello, potrò riportare divisioni al mezzo millimetro e
non oltre. Per risoluzioni maggiori occorrerà un calibro; per una maggiore
definizione un micrometro e certamente per un geometra basterà un metro laser
preciso al centimetro e
non certo un microscopio elettronico: anche se questo permette di
apprezzare milionesimi di millimetro, una simile precisione non serve (e non è
neppure applicabile) per costruire una casa.
In ogni caso, una rappresentazione digitale di una grandezza
analogica è sempre e comunque una rappresentazione approssimata, approssimata
all' ampiezza del "gradino" digitale, come lo è la misura di una
lunghezza a seconda dello strumento usato per la misura stessa.
Se torniamo all' esempio della scala e del piano inclinato, quanti più
gradini avrà la scala (discreta), tanto più si approssimerà ala piano
inclinato (continuo): per un numero infinito di gradini le due vie si
equivarranno. E tanto minore è il numero dei gradini tanto più grossolana
sarà l' approssimazione.
Insistiamo a chiarire che questo, se a prima vista pare un grosso difetto,
in generale non lo è, in quanto
|
basta che
l' approssimazione dell'
informazione sia adeguata all' uso che se ne vuol fare |
ovvero presenti un errore, o approssimazione, minore del massimo accettabile
in quella data applicazione.
Il che vale sia per misure analogiche che digitali. E questa semplice considerazione è quella su cui si basa il trattamento
digitale dei dati.
Ad esempio, misurando la
temperatura ambiente in casa, la precisione di 1 grado o mezzo grado sarà più che
sufficiente
e, di conseguenza, sapere che ci sono 27, 82 °C piuttosto che 27,5 °C non ci è
di alcuna utilità. Dunque, non serve un termometro di grandissima precisione. Questo potrà essere richiesto nel caso di altre applicazioni.
Una definizione di 8 bit permetterà 256 suddivisioni di una scala tra -40 °C e
+ 80°C, pari a circa mezzo grado.
Inoltre va tenuto conto che una
misura priva di approssimazione, anche solo per gli errori relativi al metodo e
alla strumentazione di misura, è impossibile nella pratica; si tratta
solo di ridurre l' errore entro i limiti richiesti dall' applicazione. Ne deriva che
:
| una opportuna approssimazione digitale nella valutazione di una
grandezza analogica può essere accettabile praticamente in tutti gli ambiti. |
Se
devo far rotolare qualcosa dal livello A al livello B, occorrerà che i gradini siano molto fini e il
piano inclinato sarà l' ideale. Ma se vado a piedi, scala e piano inclinato sono circa lo
stesso: basta che i gradini siano della misura adeguata.
|