Tutorials - Elettronica

La conversione AD

Quantizzazione

Se il segnale analogico può assumere infiniti valori all' interno di un determinato campo di variazione, il segnale digitale può assumere solamente un numero finito di valori discreti (digitali). La conseguenza è che gli infiniti valori del segnale analogico devono essere frazionati in un numero finito di livelli fissi, graficamente rappresentabili come gradini.
Di conseguenza, i valori intermedi della grandezza analogica compresi tra il livello di un gradino ed il successivo saranno unificati in solo valore, quello del corrispondente gradino, con una perdita di definizione.

Prendiamo l' esempio precedente di una conversione codificata su 3 bit per una tensione da 0 a 8V.

Sette comparatori ricevono all' ingresso non invertente la tensione analogica da valutare, mentre gli ingressi invertenti sono alimentati da un array di resistenze che suddividono una tensione di riferimento in ottavi.

Se la tensione di ingresso è minore della soglia del primo comparatore, la sua uscita (e quella di tutti gli altri) sarà a 0. Mentre la tensione di ingresso sale, i comparatori commutano uno dopo l' altro, portando le uscita a livello 1.

L' encoder codifica le sette uscite dei comparatori in tre linee binarie.
LSB (last significant bit) sarà il bit meno significativo (bit 0) e MSB (most significant bit) sarà il bit più significativo (bit 2).

Se la tensione di riferimento è 8V, ogni comparatore commuterà ad 1 V di differenza dal precedente.

Possiamo riportare in un grafico l’ampiezza massima del segnale d’ingresso sulle ascisse e il valore binario del risultato della conversione sulle ordinate.

Ad ogni variazione di 1 V della tensione di ingresso, si avrà lo scatto di un comparatore e quindi l' incremento di 1 bit del risultato binario.

Si nota che tutti i possibili valori, ad esempio, tra 0 e 1V sono "raggruppati" in un unico livello. Così pure tutti i possibili valori tra 1 e 2V e così via.

Questo è evidente pensando che si tratta di sette comparatori che hanno una soglia di 1V tra l' uno e l'altro, per cui i valori di tensione intermedi non potranno essere rilevati.

Ad esempio, se il segnale varia tra 0.5 e 0.75V, l' encoder codificherà 000 in ogni caso, dato che il primo comparatore commuta a 1V.

Questo processo di raggruppamento si chiama quantizzazione ed i i livelli che definiscono ciascun gradino sono i livelli di quantizzazione.
La distanza tra due livelli, ovvero l' altezza del gradino è chiamata passo di quantizzazione Q , o quanto (ricordiamo che quanto è una parola derivata dal latino quantum, quantità, ed indica una quantità finita ed indivisibile; nella fisica è sinonimo di particella).

Un dato digitale, composto da N bit, può assumere 2^N valori diversi. Ad esempio, disponendo di 3 bit si potranno codificare numeri pari a 2³ = 8.
Quindi, digitalizzando una tensione di ingresso di 8 V, il passo di quantizzazione sarà dato da:

Q = tensione / 2^N= 8 / 8 = 1 V

Digitalizzando nelle stesse condizioni una tensione di ingresso di 5V:

Q = tensione / 2^N= 5 / 8 = 0.625 V

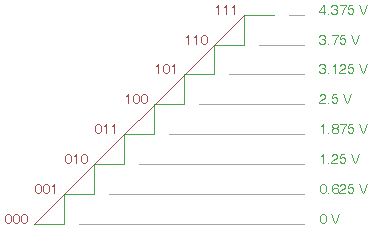Ovvero la differenza tra un gradino ed il successivo sarà 0.625 V.

E' evidente che, ad esempio, se la tensione di ingresso è di 0, 1 o 0, 2 o 0,3 V, il risultato digitale della conversione sarà sempre 0 , corrispondente al 000.
Così se i valori saranno 0,7 o 1 o 1,2 V, la conversione renderà in ogni caso il valore di 001 (corrispondente al gradino A1).

Quindi, quando un segnale che ha la possibilità di assumere infiniti valori viene convertito in un dato che dispone solo di valori finiti, si avrà un errore dovuto al fatto che ai valori intermedi tra i gradini verrà assegnato lo stesso risultato digitale.

In una tabella:

Tensione di ingresso [V]	Codifica binaria
0-0.625	000
0.625-1.25	001
1.251-1.875	010
1.875-2.5	011
2.5-3.125	100
3.125-3.75	101
3.75-4.375	110
4.375-5.00	111

In un convertitore analogico digitale, quindi, i valori d’uscita non riproducono fedelmente il segnale d’ingresso, ma ne danno una rappresentazione approssimativa, tanto più precisa quanto minore è il passo di quantizzazione Q, cioè quanto più numerosi sono i livelli di quantizzazione.

Questo errore si chiama di errore di quantizzazione ed il suo massimo valore è pari a ½ Q .
In valore assoluto sarà:

V_Q = Vfs / 2ⁿ

Quindi, con l' esempio precedente della conversione a 7 bit:

Vq = 5 / 2³ = 0.625 V

E questo è il valore dell' altezza di un gradino tra un risultato e il successivo. Ovvero, tutti i valori intermedi assunti dalla tensione di ingresso saranno cumulati nello steso gradino.

Con un altro esempio, per un fondo scala di 10V, al variare della risoluzione avremo:

Risoluzione	4	6	8	10	12	16
Errore	625 mV	156 mV	39 mV	9,8 mV	2.4 mV	153 uV

Poichè l' errore è legato al numero dei bit del risultato, quanto maggiore è questo numero, tanto minore sarà l' errore assoluto della conversione, dato che diminuisce l' altezza dei gradini e quindi la differenza di livello tra uno e l' altro. Con infiniti gradini l' errore sarebbe annullato, dato che la scala diverrebbe la retta.

Quale risoluzione è la migliore ?

Commercialmente si producono convertitori a 4, 6, 8, 10, 12, 14, 16, 18, 20 e 24 bit.

Parrebbe quindi molto meglio disporre della massima risoluzione possibile in ogni caso e che un ADC a 64 bit sia molto meglio di uno a 10 bit.

Ma non è così, perchè va ricordato che ci sono altri punti da considerare, punti che limitano l' ampiezza del dato digitale.

Innanzitutto si deve ricordare che si ha a che fare con grandezze reali in ambienti operativi reali. E che la misura è soggetta ad errori propri, sia dei mezzi con cui è effettuata, sia dovuti alla natura della grandezza da misurare. E nel campo elettrico, le tensioni indotte tra circuiti, il rumore prodotto da altre fonti elettriche vicine, ma anche da segnali elettromagnetici o dall' agitazione molecolare dei componenti del circuito limita sensibilmente la precisione teorica.
In pratica, una misura richiede un grado di precisione relativo all'applicazione per cui è fatta. Un sarto taglierà la stoffa con l' approssimazione di vari millimetri, un pezzo meccanico di precisione potrà richiede precisioni di millesimi di millimetro, l' asfaltatura di una strada avrà approssimazioni di decimetri.
Inoltre, per trattare un dato a 8 bit occorreranno risorse del sistema di elaborazione di gran lunga minori di quelle richieste da un dato a 64 bit. Quindi, una risoluzione maggiore richiederà un contemporaneo aumento delle possibilità del microcontroller o del microprocessore; e questo si riflette in un aumento sensibile dei costi.
E, quanto maggiore sarà la sua qualità, il che comprende anche la risoluzione, tanto maggiori saranno le specifiche richieste ai comparatori e alle tensioni di riferimento, influendo sui costi.

Quindi:

la precisione della conversione dovrà essere calibrata non su un valore teoricamente perfetto, ma sulla reale necessità del progetto

ed il numero dei bit del risultato sarà appunto proporzionale all' impiego che se ne deve fare.
Semplicemente, conoscendo l' ampiezza dell' errore di quantizzazione, se ne potrà tenere conto dove necessario.

Nel convertitore SAR, il risultato della conversione (ovvero l' errore di quantizzazione) dipende dal numero dei tentativi possibili (ovvero dall' ampiezza del registro SAR): maggiori sono i tentativi, minore sarà la differenza tra un tentativo e il successivo e maggiore sarà l' approssimazione con cui si ci si avvicinerà al risultato corretto.

Quantizzazione e risoluzione

In altre parole, la risoluzione è equivalente al paso di quantizzazione e corrisponde alla variazione di tensione di ingresso associata alla variazione del bit meno significativo del risultato codificato.

La risoluzione può anche essere espressa in percentuale:

risoluzione % = (risoluzione/Vin) 100 = 100 / 2ⁿ

Dobbiamo ora ricordare che ogni gradino della conversione dipende dal punto di commutazione di un comparatore e che il valore analogico in ingresso che produce la massima uscita digitale è semplicemente un qualsiasi valore superiore alla tensione di riferimento dell' ultimo comparatore (nell' esempio precedente 7V).

Se facciamo riferimento a bit del risultato binario della conversione, intendendo come unità di misura delle ascisse 1 LSB = valore di 1 bit, posiamo tracciare questo diagramma della funzione di trasferimento ideale dell' ADC:

Per una risoluzione con codifica su 3 bit il valore massimo rappresentabile è 111_bin, che è 7_dec.

Per un ingresso di Vref- la codifica digitale del risultato è 0, nel nostro esempio 000_bin
Una tensione pari a Vref+ genera il codice (2ⁿ-1), nel nostro esempio 111_bin.
Una qualsiasi tensione Vx è convertita nel codice x * (2ⁿ-1) / Vref+.

Supponendo che l' ADC abbia uscita lineare, 111_bin equivale al fondo scala (che, ricordiamo, non è necessariamente 5V o 10V o altro, ma corrisponde alla tensione di riferimento).

Quindi, il valore di ogni singolo bit che abbiamo definito come dato da:

valore di ogni step = Vfs / (2ⁿ-1)

dato che il numero dei gradini pari a 2ⁿ-1 .

Il valore della tensione analogica Vx corrispondente ad un dato risultato digitale x sarà:

Vx = Vref- + (range * x) / (2ⁿ-1)

con range = (Vref+ - Vref-).

Peraltro, si trova riportata spesso la seguente relazione:

valore di ogni step = Vfs / 2ⁿ

Se si vuole davvero essere precisi, allora si dovrebbe considerare che:

se nel diagramma precedente

sono sette i comparatori, i valori in totale sono 8, comprendendo lo zero (000).

Ci saranno dunque uscite del codificatore:

Intervallo tensione di ingresso	Codifica risultato della conversione
0-1	000
1-2	001
2-3	010
3-4	011
4-5	100
5-6	101
6-7	110
7-8	111

dato che anche il gradino che da risultato 0 non corrisponde allo 0 della tensione di ingresso, ma a tutti i valori tra lo 0 e il livello di commutazione del primo comparatore (in questo esempio,1 V) !

Quindi, per n uscite, i comparatori sono 2ⁿ-1

e che

Ogni valore binario del risultato della conversione rappresenta non un singolo valore analogico, ma un piccolo intervallo di valori

(in questo caso ampio 1V). Così quando si converte un valore di tensione, il valore binario 001 corrisponderà a tutti i valori analogici compresi tra 1 e 2 V e così via.
Ovvero tra i bordi dei due gradini che si succedono.

Quindi la prima o la seconda valorizzazione fanno solamente riferimento ad un arrotondamento: in difetto (la prima) e in eccesso (la seconda).
Per cui:

tensione_analogica = (Vfs / (2ⁿ-1)) * lettura_digitale

è relativa al bordo di uscita del gradino e:

tensione_analogica = (Vfs / 2ⁿ) * lettura_digitale

è relativa al bordo di ingresso del gradino stesso.

Vediamo in una tabella i due approcci per 2ⁿ= 1024 e Vfs = 10V

Calcolando:

valore di ogni step = Vfs / 2ⁿ = 10 / 1024 = 0.009765625 V

valore di ogni step = Vfs / (2ⁿ-1) = 10 / 1023 = 0.009775171 V

possiamo tracciare un' altra tabella, ricordando che i bit valgono 2^m dove m è la posizione nel byte.
Per cui il bit 0 vale X * 2⁰, il bit 1 vale X * 2¹, il bit 2 vale X * 2², e così via.

posizione bit	7	6	5	4	3	2	1	0
bit = Vfs / 2ⁿ	1.25 V	0.625 V	0.3125 V	0.156 V	78,125 mV	39.062 mV	19.531 mV	9.765 mV
bit = Vfs / 2ⁿ-1	1.251 V	0.625 V	0.3128 V	0.156 mV	78,201 mV	39.100 mV	19,55 mV	9.775 mV

Quindi, in funzione del risultato esadecimale della conversione:

lettura_digitale	*(10 / 1024) lettura_digitale**	(10 / 1023) * lettura_digitale
3FF_hex= 1023_dec	9.990234	10
200_hex= 512_dec	5	5.00488
1FF_hex= 511_dec	4.99023	4.99511
100_hex= 256_dec	2.5	2.50244
0FF_hex= 255_dec	2.490234	2.49266
008_hex= 8_dec	0.078125	0.078201
001_hex= 1_dec	0.00975625	0.00977517106

Vediamo come i valori calcolati per 2ⁿ-1 e per 2ⁿ siano spostati tra di loro di un valore pari all' ampiezza massima di uno step (1LSB). E, tra l' altro, 1LSB è solitamente l' errore che si attribuisce al convertitore.

Quindi, se la relazione più corretta è quella che fa riferimento a Vfs / (2ⁿ-1), entrambe le valutazioni possono essere accettabili in pratica.
E per ottenere un preciso fondo scala l' azione sarà quella di tarare opportunamente il valore della tensione di riferimento.